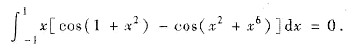问题
问答题
求
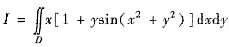，其中D是由y=x3，y=1，x=-1所围区域．
答案
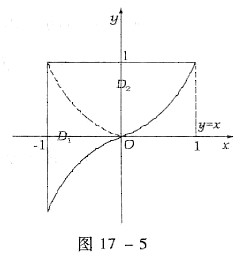
参考答案：[分析与求解一] 区域D如图17-5所示．被积函数有奇偶性，积分区域D本身关于坐标轴没有对称性，但若添加辅助线y=-x3(x≥0)，将D分解成：D=D1∪D2，其中
D1={(x，y)|-1≤x≤0，x3≤y≤-x3}，D1关于x轴对称，
D2={(x，y)|-1≤x≤1，|x|3≤y≤1}，D2关于y轴对称．
又xysin(x2+y2)对x，y均为奇函数，于是
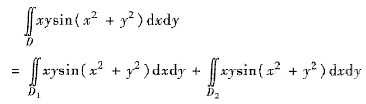
=0+0=0
因此，
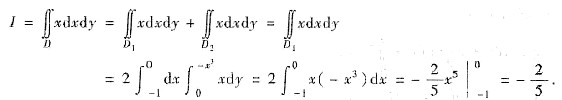
[分析与求解二] 直接化成定积分
这里利用了奇函数在对称区问上的积分性质，即
