问题
问答题
证明可微的必要条件定理：设z=f(x，y)在点(x0，y0)处可微，则f’x(x0，y0)与f’y(x0，y0)都存在，且
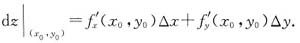
并请举例说明(2)之逆不成立．
答案
参考答案：设z=f(x，y)在点(x0，y0)处可微，则(*)式成立．命△y=0，于是
[*]
命△x→0有[*]，同理有[*]．证明了f’x(x0，y0)与f’y(x0，y0)存在，并且[*]．
例子，对于函数[*]有
[*]
f’y(0，0)=0，
两个偏导数均存在．以下用反证法证此f(x，y)在点(0，0)处不可微．若可微，则有
Δf=f(Δx，Δy)-f(0，0)=0△x+0Δy+o(ρ)，
即 [*]，
即 [*] (**)
但此式是不成立的．例如取△y=k△x，
[*]
随k而异，(**)式不成立，所以不可微．