问题
问答题
设f(x)在区间[-1，1]上存在二阶连续导数，f(0)=0，设
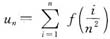，求
．
答案
参考答案：将f(x)在x=0处按拉格朗日余项泰勒公式展开至n=1，有
[*]
而 [*]
又由于f"(x)在[-1，1]上连续，故存在M＞0，对一切x∈[-1，1]，|f"(x)|≤M．于是
[*]
所以 [*]
搜题请搜索小程序“爱下问搜题”
设f(x)在区间[-1，1]上存在二阶连续导数，f(0)=0，设
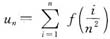，求
．
参考答案：将f(x)在x=0处按拉格朗日余项泰勒公式展开至n=1，有
[*]
而 [*]
又由于f"(x)在[-1，1]上连续，故存在M＞0，对一切x∈[-1，1]，|f"(x)|≤M．于是
[*]
所以 [*]