问题
问答题
设二阶可微函数满足方程
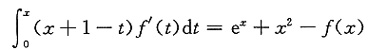
求f(x).
答案
参考答案:在所给方程两边分别对x求一阶、二阶导数以建立关于f(x)的微分方程初值问题,然后再求解,得到f(x)的表示式.
在所给方程两边关于x分别求一阶和二阶导数,得到

且
f’(0)=1/2,
f"(x)+f’(x)=ex+2-f"(x).
故得微分方程的初值问题
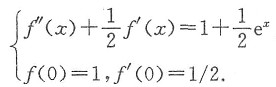 ①
①
则对应齐次方程的特征方程为λ2+λ/2=0,解得
λ1=0,λ2=-1/2.
对应齐次方程的通解为
y=c1+c2e-x/2.
令非齐次方程的一个特解为
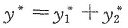 =Ax+Bex,
=Ax+Bex,
 是因为1=1·e0x,而0为特征根,故
是因为1=1·e0x,而0为特征根,故

代入方程①得到A=2,B=1/3,故
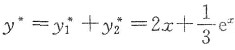
因而,原方程的通解为

由y(0)=1,f’(0)=1/2,得到
c1+c2+1/3=1,-c2/2+2+1/3=1/2,
解得c1=-3,c2=11/3,故

