问题
单项选择题
设
，则x→0时f(x)是g(x)的______．
A．高阶无穷小
B．低价无穷小
C．同阶的非等价无穷小
D．等价无穷小
答案
参考答案：B
解析： 归结为求极限
．用等价无穷小代换和洛必达法则求之．
解一
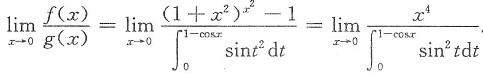
因分母为x的(2+1)×2=6阶无穷小量，而分子为x的4阶无穷小量，因而f(x)是g(x)的低阶无穷小．仅(B)入选．
解二
故f(x)为g(x)的低阶无穷小．仅(B)入选．
解三 f(x)～x4(x→0)，g(x)为(2+1)×2=6阶无穷小量(x→0)．
显然，f(x)为g(x)的低阶无穷小．仅(B)入选．