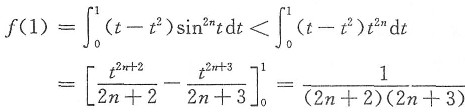问题
问答题
求证函数
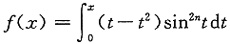 在区间(0,+∞)内的极大值不超过
在区间(0,+∞)内的极大值不超过
 ,其中n为正整数.
,其中n为正整数.
答案
参考答案:先求出f’(x),求出在(0,+∞)内最大值点,再利用sin2nt<t2n放大极(最)大值.例得证.
证 因f’(x)=(x-x2)sin2nx,当0<x<1时,f’(x)>0;当x>1时,f’(x)<0.故f(x)在(0,+∞)内的最大值为
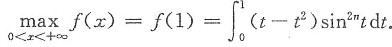
又当0<t<1时,t-t2>0;当
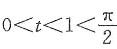 时,sint<t,有sin2nt<t2n.于是
时,sint<t,有sin2nt<t2n.于是