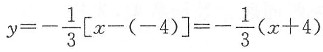问题
填空题
设f(x)为可导的以4为周期的周期函数，且
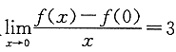，则曲线y=f(x)在点(-4，0)处的法线方程为______．
答案
参考答案：
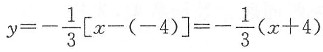
解析： 首先要了解导数的几何意义．在几何上，函数y=f(x)在点x0处的导数f’(x0)是曲线y=f(x)在点(x0，f(x0))处的切线斜率，因而y=f(x)过其上一点(x0，f(x0))的切线方程和法线方程分别为
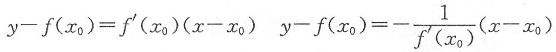
因f(x)为导数的以4为周期的周期函数，则f’(x)也是以4为周期的可导函数，即f’(-4)=f’(0)．而
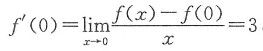
故f’(-4)=3，所以法线方程为
