问题
单项选择题
设f(x)是连续函数,F(x)是f(x)的原函数,则______.
A.当f(x)是奇函数时,F(x)必是偶函数
B.当f(x)是偶函数时,F(x)必是奇函数
C.当f(x)是周期函数时,F(x)必是周期函数
D.当f(x)是单调增函数时,F(x)必是单调增函数
答案
参考答案:A
解析: 利用f(x)的所有原函数的性质判别.
f(x)的所有原函数可写为
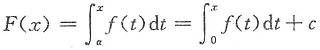 (c为任意常数).
(c为任意常数).
它有下述常用的性质:
(1)若f(x)是奇函数,则
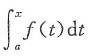 必为偶函数’
必为偶函数’
(2)若f(x)为偶函数,则只有当c=0时,
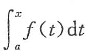 才为奇函数;
才为奇函数;
(3)若f(x)为周期函数,则存在常数T,使得对任意x,有f(x+T)=f(x),而
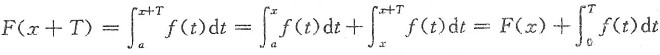
即只有
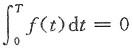 时,F(x)才是周期函数’
时,F(x)才是周期函数’
(4)若f(x)为单调增函数,对任意x1,x2,不妨设x1<x2,有f(x1)<f(x2),而
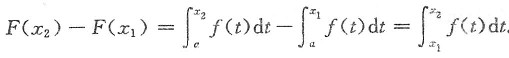
要想F(x)是单调增函数.则应有
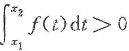 ,而由x1,x2的任意性知,必须有f(x)>0才行.
,而由x1,x2的任意性知,必须有f(x)>0才行.
解一 设
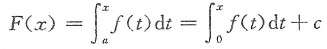 (c为任意常数),
(c为任意常数),
若f(x)为奇函数,则
f(x)=-f(x),
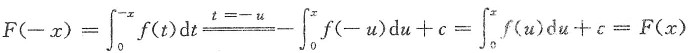
故F(x)为偶函数.仅(A)入选.
解二 令f(x)=x2,
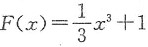 ,则可排除(B);
,则可排除(B);
令f(x)=1,F(x)=x,则可排除(C);
令f(x)=x,
 ,则可排除(D);
,则可排除(D);
故仅(A)入选.

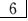 龋深,去腐质后未探及穿髓孔,叩痛(-),冷测同对照牙,探远中龈 * * 出血
龋深,去腐质后未探及穿髓孔,叩痛(-),冷测同对照牙,探远中龈 * * 出血