搜题请搜索小程序“爱下问搜题”
问题 问答题

设A是n阶矩阵，α1，α2，…，αn是n维列向量，其中αn≠0，若Aα1=α2，Aα2=α3，…，Aαn-1=αn，Aαn=0．

求A的特征值、特征向量．

答案

参考答案：利用相关矩阵的性质求之．

解析：(1)令
k1α1+k2α2+…+knαn=0．
①
由题设
Aα1=α2，Aα2=α3，…，Aαn-1=αn，
有
Anα1=An-1α2=…=Aαn=0．
将An-1左乘式①，得k1αn=0．由于αn≠0，故k1=0．
再依次用An-2，An-3，…乘式①，可得
k2=k3=…=kn=0，
所以α1，α2，…，αn线性无关．
(2)由于
A[α1，α2，…，αn]=[α2，α3，…，αn，0]


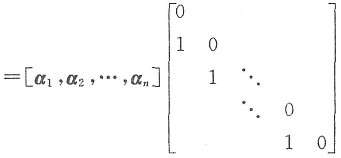
因为α1，α2，…，αn线性无关，矩阵[α1，α2，…，αn]可逆，从而


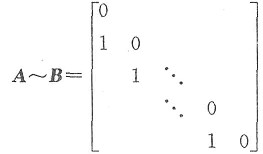
得知A的特征值全为0．又因
秩(A)=秩(B)=n-1，
所以Ax=0的基础解系由n-秩(A)=1个向量组成，由Aαn=0·αn知，A的线性无关的特征向量为αn，全部特征向量为kαn，k≠0为任意常数．

问答题

维生素C（C6H12O6）主要存在于蔬菜、水果中．它能增强人体对疾病的抵抗能力．

（1）取三片维生素C，压碎后溶于10mL水中，过滤．取少量滤液向其中滴加几滴紫色石蕊试液，试液变红，说明维生素C的水溶液呈______性．

（2）维生素C在酸性环境中比较稳定，在高温时容易被破坏．请你想一想，如何食用黄瓜，才能充分利用黄瓜中丰富的维生素C？
查看答案
阅读理解
阅读理解。
     The IOC today launched the bid process for the Games of the XXXI Olympiad in 2016. The 203 National
Olympic Committees (NOCs) have been invited to submit the name of a city within their jurisdiction as an
Applicant City to host the Games in nine years time.
     Phase Ⅰ: the candidature acceptance procedure
     This phase involves a thorough review by the IOC of each city's potential to organize the 2016 Olympic
Games. Cities will be asked to reply to a questionnaire. Their answers will be studied by the IOC in order to
help the IOC Executive Board to select the cities that will become Candidate Cities and therefore move on to
Phase Ⅱ. All relevant information and deadlines relating to the first phase are contained in the Candidature
Acceptance Procedure and Questionnaire.
     Phase Ⅱ: the candidature evaluation procedure
     Candidate Cities will be requested to submit their Candidature
File, that is to say, an in-depth description of their Olympic project,
and prepare for the visit of the IOC Evaluation Commission. The		             
 Evaluation Commission will make a detailed technical assessment of each candidature and publish a report one
month before the election of the Host City for IOC members to review.
Key dates:
13 September 2007 NOCs to inform the IOC of the name of an
Applicant City
14 January 2008 Submission of Application File and
guarantee letters to the IOC
Jan. - June 2008Examination of replies by the IOC
June 2008 IOC Executive Board acceptance of
Candidate Cities
8 - 24 August 2008 Olympic Games Observer Program-Beijing
2008
12 February 2009Submission of Candidature File to the IOC
One month before
the election of the
Host City		Report of the 2016 IOC Evaluation
Commission
2 October 2009 Election of the Host City of the 2016
Olympic Games during the 121st IOC
Session in Copenhagen
1. How can the city be admitted into PhaseⅡ?
A. By submitting the name.
B. By replying to a questionnaire.
C. By getting the IOC Executive Board's admission.
D. By submitting their Candidature File.
2. According to the passage, when will the report of the 2016 Olympics be known to the world?
A. February, 2009.
B. March, 2009.
C. September, 2009.
D. October, 2009.
3. Where will the result of the Host City of the 2016 0lympic Games be declared?
A. Beijing.
B. Copenhagen.
C. Toronto.
D. Washington.
4. How long will it take a city to succeed in the election?
A. About l year.
B. About 2 years.
C. About 3 years.
D. About 9 years.
查看答案