设参数方程
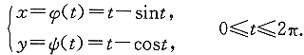
求证:
(Ⅰ)由参数方程确定连续函数y=y(x)(0≤x≤2π);
(Ⅱ)y=y(x)在[0,π]单调上升,在[π,2π]单调下降;
(Ⅲ)y=y(x)在[0,2π]是凸函数.
参考答案:(1)证明x=φ(t)在[0,2π]存在连续的反函数;
(2)证明
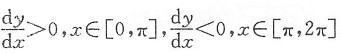
(3)证明
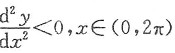
证 (Ⅰ)φ’(t)=1-cost>0(t∈(0,2π)),φ’(0)=φ’(2π)=0,
又φ(t)在[0,2π]上连续,故φ(t)在[0,2π]上单调上升,值域为
[φ(0),φ(2π)]=[0,2π],
得x=φ(t)在[0,2π]上存在连续的反函数t=t(x),定义域为[0,2π].
因此,
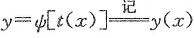 在[0,2π]上连续.
在[0,2π]上连续.
(Ⅱ)由反函数的可导性及复合函数的可导性知,y=y(x)在(0,2π)内可导,由参数式求导法,有
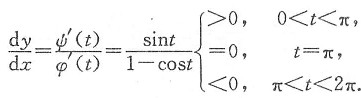
由于t∈[0,π],有x∈[0,π];t∈[π,2π],x∈[π,2π],
于是
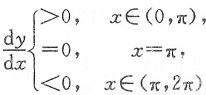
因此,y=y(x)在[0 π]上单调上升,在[π,2π]上单调下降.
(Ⅲ)由于y(x)在[0,2π]上连续,则由x∈(0,2π)时,有

(t∈(0,2π),即x∈(0,2π).y=y(x)在[0,2π]上是凸函数.
