问题
问答题
两个寡头垄断生产的行为遵循古诺模型，他们都生产一同质产品，其市场需求函数为Q=900-9P，试求：
(1)若两厂商的生产成本都为零，均衡时厂商的产量和价格为多少
(2)若两个厂商的生产成本都不为零，成本函数分别为：
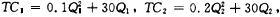，则均衡时厂商的产量和价格又为多少
答案
参考答案：(1)根据假设条件，从产品需求函数Q=900-9P中，可得，当P=0时，Q=900。根据古诺模型，当两个厂商利润极大量的产量Q＝Q1+Q2＝300+300＝600，将Q代入需求函数，得价格P=30。
(2)若厂商成本不为零，我们根据厂商追求利润最大化的原则求得厂商的均衡产量和价格。从Q＝900-10P，可得P＝90-0.1Q，而Q=Q1+Q2，所以P=90-0.101-0.1Q2。
对于厂商1来说，TR1=PQ1＝(90-0.1Q2)Q1=90Q1-[*]-0.1Q2Q1
对于厂商2来说，TR2=PQ2＝(90-0.1Q2)Q2=9002-[*]-0.1Q2Q1
两厂的利润函数分别为：
π1＝TR1-TC1＝90Q1-[*]-0.1Q2Q1-[*]-30Q1
π2＝TR2-TC2=90Q2-[*]-0.1Q2Q1-[*]-30Q2
为使利润最大化，一阶导数等于0
解得Q1=130.4，Q2=78.2，所以，Q＝Q1+Q2＝208.6