问题
填空题
设向量组α1，α2，α3线性无关，且α1+aα2+4α3，2α1+α2-α3，α2+α3线性相关，则a=（）。
答案
参考答案：E
解析：
[考点] 向量的相美性
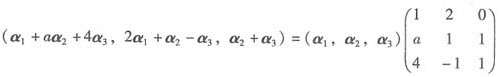，因为α1，α2，α3线性无关，而α1+aα2+4α3，2α1+α2-α3，α2+α3线性相关，所以
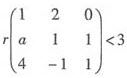，即
，解得a=5．
搜题请搜索小程序“爱下问搜题”
设向量组α1，α2，α3线性无关，且α1+aα2+4α3，2α1+α2-α3，α2+α3线性相关，则a=（）。
参考答案：E
解析：
[考点] 向量的相美性
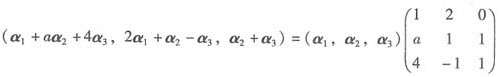，因为α1，α2，α3线性无关，而α1+aα2+4α3，2α1+α2-α3，α2+α3线性相关，所以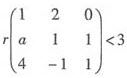，即，解得a=5．