问题
单项选择题
在具有6个顶点的无向简单图中,当边数最少为 (26) 条时,才能确保该图一定是连通图,当边数最少为 (27) 条时,才能确保该图一定是哈密尔顿图。
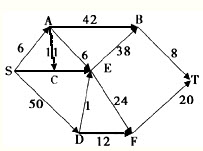
给定带权的有向图,如下图所示。设该图代表一个地区的交通图,从S到T的最短路径有 (28) 条,路径的长度是 (29) ,从S出发经过每点一次且只有一次到T的路径(哈密尔顿路径)有 (30) 条。
(30)处填()。
A.0
B.2
C.56
D.59
答案
参考答案:A
解析:
一个即不包含回路又不包含平行边的图称为简单图。如果一个无向图G的边数大于[*]为顶点个数),则G是一个连通图。依题意n=6,所以如果边数大于10,则该图为连通图。如果图G具有一条包含 G中所有顶点的回路,则称该回路为哈密尔顿回路,其相应的图叫做哈密尔顿图,当边数最少为12条时,才能确保该图一定是哈密尔顿图。
从入度为0的顶点S出发到达出度为。的顶点T的最短路径有两条,它们是:(S,A,E,F,T)和(S,A,B, T),其路径长度为56。从图中可以看出,从S出发经过每个顶点一次仅且一次到达T的路径不存在。