问题
单项选择题
如图所示，水平绷紧的传送带AB长L=6m，始终以恒定速率V1=4m/s运行。初速度大小为V2=6m/s的小物块（可视为质点）从与传送带等高的光滑水平地面上经A点滑上传送带。小物块m=lkg，物块与传送带间动摩擦因数μ=0.4，g取lom/s²。下列说法正确的是（）
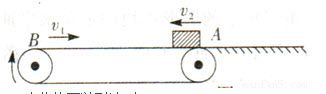
A.小物块可以到达B点
B.小物块不能到达B点，但可返回A点，返回A点速度为6m/s
C.小物块向左运动速度减为0时相对传送带滑动的距离达到最大
D.小物块在传送带上运动时，因相互间摩擦力产生的热量为50J
答案
参考答案：D
解析：
对物块受力分析，由牛顿第二定律得：μmg=ma；a=μg=0.4×10=4m/s²；当向左运动速度减为零的时候，距离最大，逆向计算：v22=2ax物；代入数据得：x物="4.5"m；此时传送带的位移：
；物块相对传送带的位移：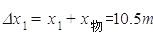
；而后物体向右加速度运动直到达到和传送带共速v1="4m/s"，此过程中物体的位移
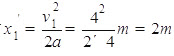；传送带的位移：
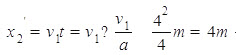，此物体相对传送带的位移最大，相对位移，
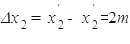相对总位移为
，
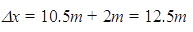产生的热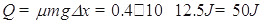
，故选项D正确；ABC错误；故选D.