问题
解答题
某一服装店销售一种进价为50元／件的衬衣，生产厂家规定售价为60～150元，当定价为60元／件时，平均每周可卖出70件，每涨价10元，一周少卖5件。
（1）若销售单价为x元／件（规定x是10的正整数倍），每周销售量为y件，写出y与x的函数关系式，并求出x的取值范围；
（2）当每件衬衣定价为多少元时，该店每周的利润最大且销售量最大，最大利润为多少？
答案
解:（1）y=70-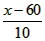
×5=100-
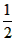x（60≤x≤150）；
（2）设利润为W，
W=（x-60）（100-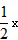
）=
+130x-6000，
a<0，W有最大值，W最大时x=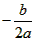
=130，
W=2450，
答：定价130元时最大利润为2450元。