问题
选择题
现有边长相等的正三角形、正方形、正六进形、正八边形形状的地砖，如果选择其中的两钟铺满平整的地面，那么选择的两种地砖形状不能是（ ）
A．正三角形与正方形
B．正三角形与正六边形
C．正方形与正六边形
D．正方形与正八边形
答案
答案：C
A、正三角形的每个内角是60°，正方形的每个内角是90°，∵3×60°+2×90°=360°，成立．
B、正六边形的每个内角是120°，正三角形的每个内角是60度．∵2×120°+2×60°=360°，或120°+4×60°=360度，成立．
C、正方形的每个内角是90°，正六边形的每个内角是120°，90m+120n=360°，m=4-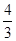
n，显然n取任何正整数时，m不能得正整数，故不能铺满；
D、正方形的每个内角为90度，正八边形的每个内角为135度，因为90+135×2=360度，成立．
故选C．