问题
问答题
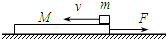
如图所示,质量M=8kg的长木板放在光滑水平面上,在长木板的右端施加一水平恒力F=8N,当长木板向右运动速率达到v1=10m/s时,在其右端有一质量m=2kg的小物块(可视为质点)以水平向左的速率v2=2m/s滑上木板,物块与长木板间的动摩擦因数μ=0.2,小物块始终没离开长木板,g取10m/s2,求:
(1)经过多长时间小物块与长木板相对静止;
(2)长木板至少要多长才能保证小物块始终不滑离长木板;
(3)上述过程中长木板对小物块摩擦力做的功.
答案
(1)小物块的加速度为a2=μg=2m/s2,水平向右
长木板的加速度为:a1=
=0.5 m/s2 水平向右F-μmg M
令刚相对静止时他们的共同速度为v,以木板运动的方向为正方向
对小物块有:v=-v2+a2t
对木板有:v=v1+a1t
联立解得:t=8s;v=14m/s
故经过8s小物块与长木板保持相对静止.
(2)此过程中小物块的位移为:
x2=
t=48m-v2+v 2
长木板的位移为:x1=
t=96mv1+v 2
所以长木板的长度至少为:L=x1-x2=48m.
故长木板至少的长度为48m.
(3)由功的公式有:Wf=f•L=umgL=0.2×2×10×48J=192J.
答:(1)经过0.8s小物块与长木板相对静止;
(2)长木板至少要48m才能保证小物块始终不滑离长木板;
(3)上述过程中长木板对小物块摩擦力做的功为192J.
