解：（1）由题意知，S_n=2ⁿ⁺²-4，

n≥2时，a_n=S_n-S_n-1=2ⁿ⁺²-2ⁿ⁺¹=2ⁿ⁺¹，

当n=1时，a₁=S₁=2³-4=4，也适合上式，

∴数列{a_n}的通项公式为a_n=2ⁿ⁺¹，n∈N*。

（2）∵b_n=a_nlog₂a_n=（n+1）·2ⁿ⁺¹，

∴T_n=2·2²+3·2³+4·2⁴+…+n·2ⁿ+（n+1）·2ⁿ⁺¹，①

2T_n=2·2³+3·2⁴+4·2⁵+…+n·2ⁿ⁺¹+（n+1）·2ⁿ⁺² ②

②-①，得T_n=-2³-2³-2⁴-2⁵-…-2ⁿ⁺¹+（n+1）·2ⁿ⁺²=-2³-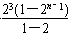+（n+1）·2ⁿ⁺²

=-2³-2³（2^n-1-1）+（n+1）·2ⁿ⁺²=（n+1）·2ⁿ⁺²-2³·2^n-1=（n+1）·2ⁿ⁺²-2ⁿ⁺²=n·2ⁿ⁺²。