如图所示,抗震救灾运输机在某场地卸放物资时,通过倾角θ=30°的固定的光滑斜轨道面进行.有一件质量为m=2.0kg的小包装盒,由静止开始从斜轨道的顶端A滑至底端B,然后又在水平地面上滑行一段距离停下,若A点距离水平地面的高度h=5.0m,重力加速度g取10m/s2,求:
(1)包装盒由A滑到B经历的时间:
(2)若地面的动摩擦因数为0.5,包装盒在水平地面上还能滑行多远?(不计斜面与地面接触处的能量损耗)
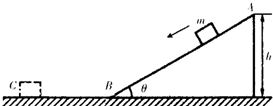
(1)包装盒沿斜面下滑受到重力和斜面支持力,由牛顿第二定律,得mgsinθ=ma
a=gsinθ=5.0m/s2
包装盒沿斜面由A到B的位移为SAB=
=10m h sin30°
包装盒由A到B做匀加速运动的时间为t
SAB=
at2得1 2
t=
=2.0s 2SAB a
(2)由动能定理得:
-fs=0-
mvB2 1 2
其中滑动摩擦力f=μmg
在B点速度vB=at
代入已知,得s=10m
答:(1)包装盒由A滑到B经历的时间是2.0s
(2)包装盒在水平地面上还能滑行10m.
