问题
解答题
已知直线l的参数方程是
(I)求圆心C的直角坐标; (II)由直线l上的点向圆C引切线,求切线长的最小值. |
答案
(I)∵ρ=
cosθ-2
sinθ,∴ρ2=2
ρcosθ-2
ρsinθ,2
∴圆C的直角坐标方程为x2+y2-
x+2
y=0,2
即(x-
)2+(y+2 2
)2=1,∴圆心直角坐标为(2 2
,-2 2
).(5分)2 2
(II)∵直线l的普通方程为x-y+4
=0,2
圆心C到直线l距离是
=5,|
+2 2
+42 2
|2 2
∴直线l上的点向圆C引的切线长的最小值是
=252-12
(10分)6

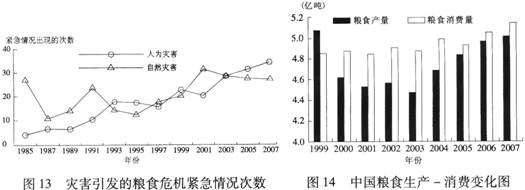
 (1)1993年以前,世界粮食不安全的主要原因是 ____ 。1993年, __引发粮食危机紧急情况的次数大于 __;其后两者交替上升。
(1)1993年以前,世界粮食不安全的主要原因是 ____ 。1993年, __引发粮食危机紧急情况的次数大于 __;其后两者交替上升。