问题
解答题
某中学举行“中国梦,我的梦”演讲比赛,九年级(1)班的班长和学习委员都想去,于是他们用摸球游戏决定谁去参加,游戏规则是:在一个不透明的袋子里有除数字外完全相同的4个小球,上面分别标有数字1,2,3,4,一人先从袋中随机摸出一个小球,另一个人再从袋中剩下的3个小球中随机摸出一个小球。
(1)请列出所有可能出现的结果;(可考虑用树形图、列表等方法)
(2)若摸出的两个小球上的数字和为偶数,则班长去参赛,请问他能如愿的概率是多少?
答案
(1)结果见解析;(2)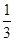 .
.
题目分析:(1)列表得出所有等可能的情况数;
(2)找出数字之和为偶数的情况数,即可求出所求概率.
试题解析:(1)列表如下:
| 1 | 2 | 3 | 4 | |
| 1 | --- | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | --- | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | --- | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | --- |
(2)两个小球上的数字和为偶数的为(3,1),(4,2),(1,3),(2,4)共4种,
则P(之和为偶数)=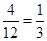 .
.
考点: 列表法与树状图法.