问题
解答题
已知等差数列{an}的首项为a,公差为b,等比数列{bn}的首项为b,公比为a,n=1,2,…,其中a,b均为正整数,且a1<b1<a2<b2<a3.
(Ⅰ)求a的值;
(Ⅱ)若对于{an},{bn},存在关系式am+1=bn,试求b的值;
(Ⅲ)对于满足(Ⅱ)中关系式的am,试求a1+a2+…+am.
答案
解:(I)由题设知,an=a+(n﹣1)b,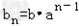
由已知可得,a<b<a+b<ab<a+2b
∴b<ab,a>1
∴ab<a+2b<3b
又∵b>0
∴a<3
∵a为正整数
∴a=2
(II)am+1=bn,可得a+(m﹣1)+1=ban﹣1
∵a=2
∴3+(m﹣1)b=b●2n﹣1
则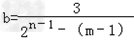
∴b>a=2且b为正整数
∴2n﹣1﹣(m﹣1)=1
∴b=3
(III)由(II)知,m=2n﹣1,an=3n﹣1
∴a1+a2+…+am=(3●1﹣1)+(3●2﹣1)+…(3●2n﹣1﹣1)
=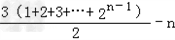
=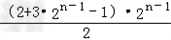
=3●22n-3+2n-2
