问题
解答题
已知正项数列{an}的前n项和为Sn,且满足Sn+an=1,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足bn=(n-2)an,且数列{bn}的前n项和为Tn,求证:数列{2nTn}为等差数列。
答案
解:(Ⅰ)由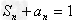 ,
,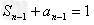 ,
,
两式相减得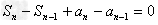
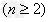 ,
,
又由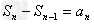 ,
,
可得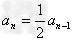
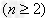 ,
,
根据 ,
,
得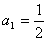 ,
,
所以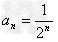 ;
;
(Ⅱ)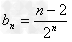 ,
,
对数列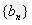 进行错位相减法得到
进行错位相减法得到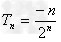 ,
,
于是数列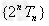 ,就是数列{-n}显然就是一等差数列。
,就是数列{-n}显然就是一等差数列。
已知正项数列{an}的前n项和为Sn,且满足Sn+an=1,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足bn=(n-2)an,且数列{bn}的前n项和为Tn,求证:数列{2nTn}为等差数列。
解:(Ⅰ)由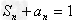 ,
,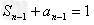 ,
,
两式相减得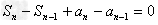
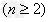 ,
,
又由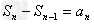 ,
,
可得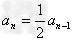
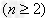 ,
,
根据 ,
,
得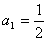 ,
,
所以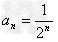 ;
;
(Ⅱ)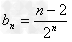 ,
,
对数列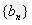 进行错位相减法得到
进行错位相减法得到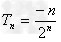 ,
,
于是数列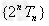 ,就是数列{-n}显然就是一等差数列。
,就是数列{-n}显然就是一等差数列。