答案：D

题目分析：根据题意得出到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点，画出图形后根据线段垂直平分线定理得出PA=PC，PC=PB，推出PA=PC=PB即可．

到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点，理由是：

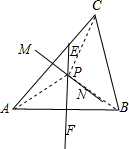
∵P在AB的垂直平分线EF上，

∴PA=PB，

∵P在AC的垂直平分线MN上，

∴PA=PC，

∴PA=PC=PB，

即P是到三角形三个顶点的距离相等的点．

故选D．

点评：解答本题的关键是注意：线段垂直平分线的交点到三角形三个顶点的距离相等，而三角形三个角平分线的交点到三角形三边的距离相等．