问题
解答题
设{an}是公比大于1的等比数列，Sn为数列{an}的前n项和．已知S3=7，且a1+3，3a2，a3+4构成等差数列．
（1）求数列{an}的通项公式．
（2）令bn=lna3n+1，n=1，2，…，求数列{bn}的前n项和Tn．
答案
解：（1）由已知得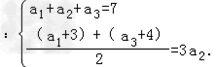
解得a2=2．
设数列{an}的公比为q，
由a2=2，可得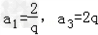
．
又S3=7，可知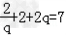
，
即2q2﹣5q+2=0，解得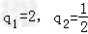
由题意得q＞1，
∴q=2∴a1=1．
故数列{an}的通项为an=2n﹣1．
（2）由于bn=lna3n+1，n=1，2，…，
由（1）得a3n+1=23n
∴bn=ln23n=3nln2
又bn+1﹣bn=3ln2n
∴{bn}是等差数列．
∴Tn=b1+b2+…+bn=
=
=
．
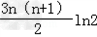故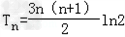
．