问题
解答题
已知数列{bn}（n∈N*）是递增的等比数列，且b1，b3为方程x2-5x+4=0的两根，
（1）求数列{bn}的通项公式；
（2）若an=log2bn+3，求证：数列{an}是等差数列；
（3）在（2）的条件下，若a1+a2+a3+…+am≤a40（m∈N*），求m的最大值。
答案
解：（1）∵b1，b3为方程x2-5x+4=0的两个根，且bn+1＞bn，
∴b1=1，b3=4，∴b22=b1b3=4，
又bn+1＞bn(n∈N*)，∴b2=2，
∴q=2，bn=2n-1；
（2）∵an=log2bn+3=log22n-1+3=n+2，
∴数列{an}是首项为3，公差为1的等差数列；
（3）由（2）知a1+a2+…+am=m×3+
×1=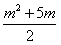
，
∴
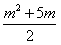≤42，整理得m2+5m-84≤0，
又m≥1，
∴1≤m≤7，∴m的最大值是7。