问题
解答题
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-l,-2和-3.小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B布袋中随机取出一个小球,记录其标有的数字为b,这样就确定点Q的一个坐标为(a,b).
⑴用列表或画树状图的方法写出点Q的所有可能坐标;
⑵求点Q落在直线y=x-3上的概率.
答案
(1)(1,-1),(1,-2),(1,-3),(2,-1),(2,-2),(2,-3);(2)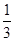 .
.
题目分析:(1)首先根据题意画树状图,根据树状图可以求得点Q的所有可能坐标;
(2)根据(1)中的树状图,求得点Q落在直线y=x-3上的情况,根据概率公式即可求得答案.
试题解析:(1)画树状图得:
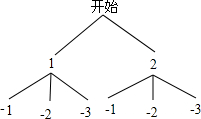
∴点Q的坐标有(1,-1),(1,-2),(1,-3),(2,-1),(2,-2),(2,-3);
(2)∵点Q落在直线y=x-3上的有(1,-2),(2,-1),
∴“点Q落在直线y=x-3上”记为事件A,
∴P(A)=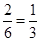 ,
,
即点Q落在直线y=x-3上的概率为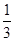 .
.
考点: 1.列表法与树状图法;2.一次函数图象上点的坐标特征.
