解：（1）由题知，S_n﹣1是a_n与﹣3的等差中项．

∴2S_n﹣1=a_n﹣3

即a_n=2S_n﹣1+3（n≥2，n∈N^*）

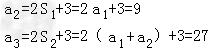
a₄=2S₃+3=2（a₁+a₂+a₃）+3=81

（2）由a_n=2S_n﹣1+3（n≥2，n∈N^*）①a_n+1=2S_n+3（n∈N^*）②

②﹣①得a_n+1﹣a_n=2（S_n﹣S_n﹣1）=2a_n

即a_n+1=3a_n（n≥2，n∈N^*）③

∴a₂=3a₁也满足③式   即a_n+1=3a_n（n∈N^*）

∴{a_n}是以3为首项，3为公比的等比数列．

∴a_n=3ⁿ（n∈N^*）