问题
解答题
已知递增的等比数列{an}满足a3=8,且a3+2是a2,a4的等差中项.
( I)求数列{an}的通项公式;
( II)若bn=log2an+1,Sn是数列{bn}的前n项和,求S20的值.
答案
解:(Ⅰ)设等比数列{an}的公比为q,依题意有
2(a3+2)=a2+a4,
∴a3=8.
∴a2+a4=20.
于是有  ,
,
解得 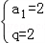 或
或 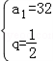 ,
,
又{an}是递增的,
故a1=2,q=2.
所以an=2n.
(Ⅱ)∵an=2n.
∴an+1=2n+1,
∵bn=log2an+1,
∴bn=log22n+1=n+1,
∴S20=2+3+4+5+…+21
=
=230.
