问题
解答题
已知函数f(x)=x2+(3a-2)x+a+1。
(1)若f(x)在区间[-1,3]上是单调增函数,求实数a的取值范围;
(2)是否存在这样的实数a,使函数f(x)在区间[-1,3]上与x轴恒有零点,若存在,求出实数a的取值范围;若不存在,说明理由。
答案
解:(1)要使f(x)在[-1,3]上是增函数,则只须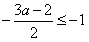 ,∴
,∴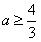 ;
;
(2)设存在这样的实数a,
则由题意知: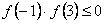 或
或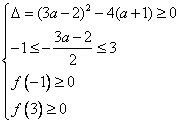 ,
,
解之得: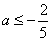 或a≥2或
或a≥2或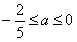 ,即a≤0或a≥2,
,即a≤0或a≥2,
∴实数a的取值范围是(-∞,0]∪[2,+∞)。
