问题
解答题
设{an}和{bn}均为无穷数列．
（1）若{an}和{bn}均为等比数列，试研究：{an+bn}和{anbn}是否是等比数列？请证明你的结论；若是等比数列，请写出其前n项和公式．
（2）请类比（1），针对等差数列提出相应的真命题（不必证明），并写出相应的等差数列的前n项和公式（用首项与公差表示）．
答案
解：（1）①设cn=an+bn，则
﹣（
+
）（
+
）
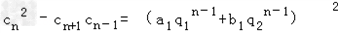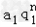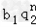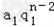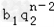=a1b1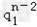
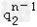（q1﹣q2）2
当q1=q2时，对任意的n∈N，n≥2，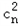
=c n+1 c n﹣1恒成立，
故{an+bn}为等比数列；
∴Sn=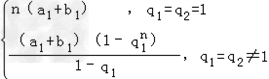
当q1≠q2时，对任意的n∈N，n≥2，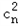
≠c n+1 c n﹣1，{an+bn}不是等比数列．
②设dn=anbn，对于任意n∈N*，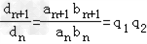
，{anbn}是等比数列．
Sn=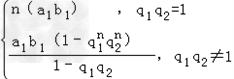
（2）设{an}，{bn}均为等差数列，公差分别为d1，d2，则：
①{an+bn}为等差数列；Sn=（a1+b1）n+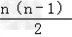
（d1+d2）
②当d1与d2至少有一个为0时，{anbn}是等差数列，
若d1=0，Sn=a1b1n+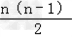
a1d2；
若d2=0，Sn=a1b1n+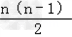
b1d1．
③当d1与d2都不为0时，{anbn}一定不是等差数列．