在真空中水平放置平行板电容器,两极板间有一个带电油滴,电容器两板间距为d,当平行板电容器的电压为U0时,油滴保持静止状态,如图所示.当给电容器突然充电使其电压增加△U1,油滴开始向上运动;经时间△t后,电容器突然放电使其电压减少△U2,又经过时间△t,油滴恰好回到原来位置.假设油滴在运动过程中没有失去电荷,充电和放电的过程均很短暂,这段时间内油滴的位移可忽略不计.重力加速度为g.试求:
(1)带电油滴所带电荷量与质量之比;
(2)第一个△t与第二个△t时间内油滴运动的加速度大小之比;
(3)△U1与△U2之比.
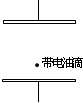
(1)油滴静止时 mg=qU0 d
则
=q m dg U0
(2)设第一个△t内油滴的位移为x1,加速度为a1,第二个△t内油滴的位移为x2,加速度为a2,则
x1=
a1△t2,x2=v1△t-1 2
a2△t2,1 2
且 v1=a1△t,x2=-x1
解得 a1:a2=1:3
(3)油滴向上加速运动时:q
-mg=ma1,即qU0+△U1 d
=ma1△U1 d
油滴向上减速运动时mg-q
=ma2,即qU0+△U1-△U2 d
=ma2△U2-△U1 d
则
=△U1 △U2-△U1 1 3
解得
=△U1 △U2 1 4
