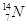(选修4-4:坐标系与参数方程)已知曲线C的参数方程是
(Ⅰ)求曲线C普通方程; (Ⅱ)若点A(ρ1,θ),B(ρ2,θ+
|
(Ⅰ)∵直线l的参数方程是
(t为参数),消去参数t得x+y=2,令y=0,得x=2.x=3+t y=-1-t
∵曲线C的参数方程是
(φ为参数,a>0),消去参数φ得x=acosφ y=
sinφ3
+x2 a2
=1,y2 3
把点(2,0)代入上述方程得a=2.
∴曲线C普通方程为
+x2 4
=1.y2 3
(Ⅱ)∵点A(ρ1,θ),B(ρ2,θ+
),C(ρ3,θ+2π 3
)在曲线C上,即A(ρ1cosθ,ρ1sinθ),B(ρ2cos(θ+4π 3
),ρ2sin(θ+2π 3
)),C(ρ3cos(θ+2π 3
),ρ3sin(θ+4π 3
))在曲线C上,4π 3
∴
+1 |OA|2
+1 |OB|2
=1 |OC|2
+1 ρ12
+1 ρ22
=1 ρ32
(cos2θ+cos2(θ+1 4
)+cos2(θ+2π 3
))+4π 3
(sin2θ+sin2(θ+1 3
)+sin2(θ+2π 3
))4π 3
=
(1 4
+1+cos2θ 2
+1+cos(2θ+
)4π 3 2
)+1+cos(2θ+
)8π 3 2
(1 3
+1-cos2θ 2
+1-cos(2θ+
)4π 3 2
)1-cos(2θ+
)8π 3 2
=
+3+cos2θ-cso(2θ+
)+cos(2θ-π 3
)π 3 8 3-cos2θ+cos(2θ+
)-cos(2θ+π 3
)2π 3 6
=
+3 8
=3 6
.7 8


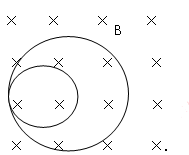
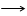
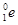 +
+ 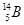
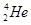 +
+ 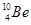
 +
+ +
+