如图所示,水平传送带A、B两端点相距x=4m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )
A.所用的时间是
s2
B.所用的时间是2.25s
C.划痕长度是4m
D.划痕长度是0.5m
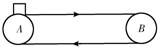
煤块在传送带上滑动时,根据牛顿第二定律有:
mgμ=ma
因此解得a=4m/s2.
当煤块速度和传送带速度相同时,位移为:
s1=
=0.5m<4mv 20 2a
因此煤块先加速后匀速运动:
加速时间为:t1=
=v0 a
=0.5s2m/s 4m/s2
匀速时间为:t2=
=x-s1 v0
=1.75s(4-0.5)m 2m/s
小煤块从A运动到B的过程中总时间为:t=t1+t2=2.25s,故A错误,B正确;
在加速阶段产生相对位移即产生划痕,固有:
△s=v0t1-s1=0.5m,故C错误,D正确.
故选BD.

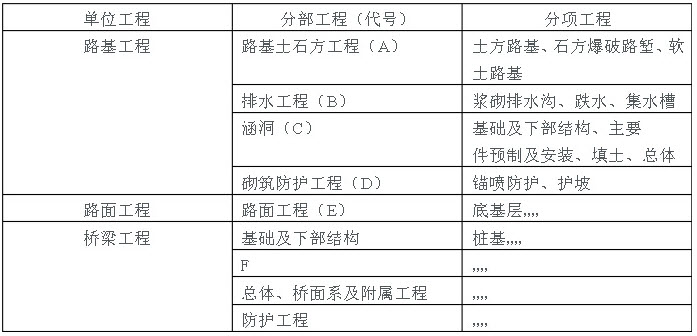 本项目中的桥梁工程为一座3×25m简支梁桥,梁板采用预制构件。 根据施工组织安排,排水工程(B)开始施工20天后才能开始路基土石方工程(A)施工,涵洞(C)完成后20天才能开始路基土石方工程(A)施工,而砌筑防护工程(D)与涵 洞(C)、排水工程(B)同时开始施工,在路基工程全部完成后才能进行路面工程(E)施工。 在本项目施工组织设计中,项目机构组成人员中的主要领导包括:项目经理1名,项目副经理1名,总工1名,党支部书记1名,财务主管1名,技术主管1名。 为搞好廉政建设,在项目管理文件中还写明了廉政建设的具体措施。 问题
本项目中的桥梁工程为一座3×25m简支梁桥,梁板采用预制构件。 根据施工组织安排,排水工程(B)开始施工20天后才能开始路基土石方工程(A)施工,涵洞(C)完成后20天才能开始路基土石方工程(A)施工,而砌筑防护工程(D)与涵 洞(C)、排水工程(B)同时开始施工,在路基工程全部完成后才能进行路面工程(E)施工。 在本项目施工组织设计中,项目机构组成人员中的主要领导包括:项目经理1名,项目副经理1名,总工1名,党支部书记1名,财务主管1名,技术主管1名。 为搞好廉政建设,在项目管理文件中还写明了廉政建设的具体措施。 问题