问题
解答题
在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线ρ=2sinθ与ρcosθ=1的交点Q的极坐标.
答案
(
,
)
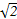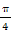以极点为坐标原点,极轴为x轴的正半轴建立直角坐标系,
则曲线ρ=2sinθ可化为:x2+(y-1)2=1,
曲线ρcosθ=1可化为x=1,
由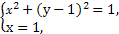
可得交点坐标为(1,1),
所以交点Q的极坐标是(,).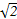
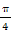搜题请搜索小程序“爱下问搜题”
在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线ρ=2sinθ与ρcosθ=1的交点Q的极坐标.
(,)
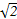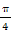以极点为坐标原点,极轴为x轴的正半轴建立直角坐标系,
则曲线ρ=2sinθ可化为:x2+(y-1)2=1,
曲线ρcosθ=1可化为x=1,
由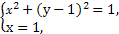可得交点坐标为(1,1),
所以交点Q的极坐标是(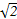,).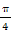