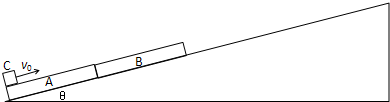
如图所示,在固定的粗糙斜面上依次放有两块质量相等m1=m2=10kg的平板A、B,长度均为 L=1.6m,斜面倾角很小为θ(sinθ=0.1,cosθ≈1),一个质量为m3=20kg 的小滑块C以v0=5m/s的初速度滑上平板A的上表面.A与斜面之间的动摩擦因素为μ1=0.2,B与斜面之间的动摩擦因素μ2=0.1,滑块C与平板A、B之间的动摩擦因数相同,设为μ3.设最大静摩擦力与相对应的滑动摩擦力大小相等,g=10m/s.
(1)若小滑块C滑上平板A时,平板均不动,而滑上平板B时,平板B开始滑动,求μ3应满足的条件;
(2)若μ3=0.4,求滑块C从开始滑上平板A到最终相对斜面静止时运动的时间和平板B沿斜面上滑的最大距离.
(1)要使小滑块滑上平板A时,平板不动,则:
μ3m3gcosθ≤μ1(m1+m3)gcosθ+μ2m2gcosθ+(m1+m2)gsinθ
要使小滑块滑上平板B时,平板B开始滑动,则:
μ3m3gcosθ≥μ2(m2+m3)gcosθ+m2gsinθ
解得:0.2≤μ≤0.45
即μ3应满足的条件为0.2≤μ≤0.45.
(2)设C在A上滑动时,C的加速度为ac,经t1时间滑出A时的速度为v1,则
m3gsinθ+μ3m3gcosθ=m3ac
解得
ac=5m/s2
根据速度位移公式,有
v02-v12=2acL
解得
v1=3m/s
根据速度时间公式,有
v0-v1=act1
解得
t1=
s2 5
C滑到B上以后,B开始滑动,加速度为aB,假设经t2时间后B、C达到共同速度v2时C还没有从B上滑出
对B:μ3m3gcosθ-μ2(m2+m3)cosθ-m2gsinθ=m2aB
解得
aB=4m/s2
根据速度位移公式,有
v2=aBt2
对C:v2=v1-act2
解得:v2=
m/s4 3
t2=
s1 3
C相对于B滑动的距离△x=
t2-v1+v2 2
t2v2 2
△x=0.5m<L假设成立
之后C和B一起沿斜面减速,加速度为a,经t3速度变为零
对BC整体:(m1+m3)gsinθ+μ2(m1+m3)gcosθ=(m1+m3)a
解得
a=2m/s2
根据速度位移公式,有
t3=v2 a
故t3=
s2 3
由于(m1+m3)gsinθ=μ2(m1+m3)gcosθ,故BC最终静止在斜面上;
故C从开始滑上平板A最终相对斜面静止时运动的时间:t=t1+t2+t3t=1.4s,平板B沿斜面上滑的最大距离:xB=
(t2+t3)xB=0.67m.v2 2