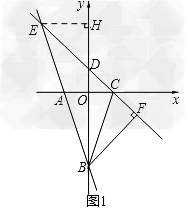
已知A(﹣1,0),B(0,﹣3),点C与点A关于坐标原点对称,经过点C的直线与y轴交于点D,与直线AB交于点E,且E点在第二象限.
(1)求直线AB的解析式;
(2)若点D(0,1),过点B作BF⊥CD于F,连接BC,求∠DBF的度数及△BCE的面积;
(3)若点G(G不与C重合)是动直线CD上一点,且BG=BA,试探究∠ABG与∠ACE之间满足的等量关系,并加以证明.
解:(1)依题意,设直线AB的解析式为 y=kx﹣3
∵A(﹣1,0)在直线上,
∴0=﹣k﹣3.
∴k=﹣3.
∴直线AB的解析式为y=﹣3x﹣3.
(2)如图1,依题意,C(1,0),OC=1.由D(0,1),得OD=1.
在△DOC中,∠DOC=90°,OD=OC=1.可得∠CDO=45°.
∵BF⊥CD于F,
∴∠BFD=90°.
∴∠DBF=90°﹣∠CDO=45°.
可求得直线CD的解析式为y=﹣x+1 由 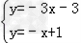 解得
解得 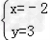
∴直线AB与CD的交点为E(﹣2,3).
过E作EH⊥y轴于H,则EH=2.
∵B(0,﹣3),D(0,1),
∴BD=4.
∴S△BCE=S△BDE+S△BDC=  ×4×2+
×4×2+  ×4×1=6
×4×1=6
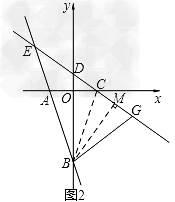
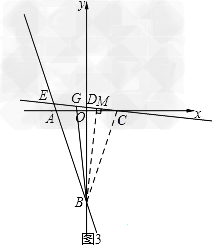
(3)连接BC,作BM⊥CD于M.
∵AO=OC,BO⊥AC,
∴BA=BC.
∴∠ABO=∠CBO.
设∠CBO=α,则∠ABO=α,∠ACB=90°﹣α.
∵BG=BA,
∴BG=BC.
∵BM⊥CD,
∴∠CBM=∠GBM.
设∠CBM=β,则∠GBM=β,∠BCG=90°﹣β.
(i) 如图2,当点G在射线CD的反向延长线上时,
∵∠ABG=2α+2β=2(α+β) ∠ECA=180°﹣(90°﹣α)﹣(90°﹣β)=α+β
∴∠ABG=2∠ECA.
(ii) 如图3,当点G在射线CD的延长线上时,
∵∠ABG=2α﹣2β=2(α﹣β) ∠ECA=(90°﹣β)﹣(90°﹣α)=α﹣β
∴∠ABG=2∠ECA.
综上,∠ABG=2∠ECA.