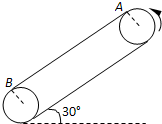
如图所示,皮带传动装置与水平面夹角为30°,轮半径R=
m,两轮轴心相距L=3.75m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑.一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=1 2π
.g取10m/s2.3 6
(1)当传送带沿逆时针方向以v1=3m/s的速度匀速运动时,将小物块无初速地放在A点后,它运动至B点需多长时间?(计算中可取
≈16,252
≈20)396
(2)小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小
物块无初速地放在A点,运动至B点飞出.要想使小物块在传送带上留下的痕迹最长,传送带匀速运动的速度v2至少多大?
(1)当小物块速度小于3m/s时,小物块受到竖直向下的重力、垂直传送带向上的支持力和沿传送带斜向下的摩擦力作用,做匀加速直线运动,设加速度为a1,根据牛顿第二定律
mgsin30°+μmgcos30°=ma1①
解得 a1=7.5m/s2
当小物块速度等于3m/s时,设小物块对地位移为L1,用时为t1,根据匀加速直线运动规律得
t1=
②v1 a1
L1=
③v12 2a1
代入解得 t1=0.4 s L1=0.6 m
由于L1<L 且μ<tan30°,当小物块速度等于3m/s时,小物块将继续做匀加速直线运动至B点,设
加速度为a2,用时为t2,根据牛顿第二定律和匀加速直线运动规律得
mgsin30°-μmgcos30°=ma2④
解得 a2=2.5m/s2
又L-L1=v1t2+
a2t22⑤1 2
解得 t2≈0.8 s
故小物块由静止出发从A到B所用时间为 t=t1+t2=1.2s
(2)传送带匀速运动的速度越大,小物块从A点到B点用时越短,当传送带速度等于某一值v′时,小物块将从A点一直以加速度a1做匀加速直线运动到B点,所用时间最短,设用时t0,即
L=
a1t02⑥1 2
解得t0=1s
传送带的速度继续增大,小物块从A到B的时间保持t0不变,而小物块和传送带之间的相对路程继续增大,小物块在传送带上留下的痕迹也继续增大;当痕迹长度等于传送带周长时,痕迹为最长Smax.
设此时传送带速度为v2,则
Smax=2L+2πR⑦
Smax=v2t0-L ⑧
联立⑥⑦⑧解得 v2=12.25m/s
答:
(1)将小物块无初速地放在A点后,它运动至B点需1.2s时间.
(2)要想使小物块在传送带上留下的痕迹最长,传送带匀速运动的速度v2至少为12.25m/s.
