问题
解答题
（本题满分12分）如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC。
（1）求证：FB＝FC；
（2）若AB是△ABC的外接圆的直径，∠EAC ＝120°，BC＝6，求AD的长。
答案
证明：见解析；（2）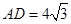
.
本试题主要是考查了圆内的性质的运用，以及直角三角形中边角关系的综合运用。
（1）因为AD平分∠EAC，所以∠EAD＝∠DAC.
因为四边形AFBC内接于圆，所以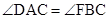
，所以
，
所以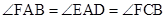
，所以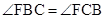FB＝FC.
（2）因为AB是△ABC的外接圆的直径，则所对的圆周角为直角，然后利用圆周角定理得到边长。
证明：因为AD平分∠EAC，所以∠EAD＝∠DAC.
因为四边形AFBC内接于圆，所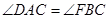以
，所以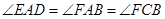
，
所以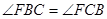
，所以FB＝FC.
（2）解：因为AB是△ABC的外接圆的直径，所以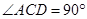
.
因为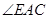
=
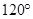，所以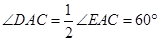
，
.
在Rt△ACB中，因为BC＝6，
，所以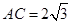
.
又在Rt△ACD中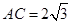，，，所以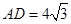.