答案：C

题目分析：延长AD到E，使AD=DE，可构造平行四边形ABEC，从而BE=AC，在△ABE中运用第三边的长度应是大于两边的差而小于两边的和，求得对角线AE的取值范围，从而得出AD的取值范围．如图，延长AD到E，使AD=DE，∵AD是BC边上的中线，∴BD=DC∴四边形ABEC是平行四边形∴BE=AC=4在△ABE中，根据三角形的三边关系，得2＜AE＜10，即2＜AE＜10．∵AD是BC边上的中线，∴AD=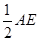∴AD的取值范围是1＜AD＜5．故答案为C．

点评：本题需要理解的是如何根据已知的两条边求第三边的范围，灵活运用平行四边形的性质和三角形的三边关系是解题的关键．