问题
问答题 计算题
甲、乙两车在平直公路上比赛，某一时刻，乙车在甲车前方L1＝11m处，乙车速度v乙＝60m/s，甲车速度v甲＝50m/s，此时乙车离终点线尚有L2＝600m，如图5所示，若甲车加速运动，加速度a＝2m/s2，乙车速度不变，不计车长．求：
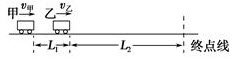
（1）经过多长时间甲、乙两车间距离最大，最大距离是多少？
（2）到达终点时甲车能否超过乙车？
答案
参考答案：
（1）5s；36m
（2）不能
解析：
（1）当甲、乙两车速度相等时，两车间距离最大，即v甲＋at1＝v乙，
得t1＝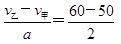
s＝5s
甲车位移x甲＝v甲t1＋
＝275m
乙车位移x乙＝v乙t1＝60×5m＝300m
此时两车间距离Δx＝x乙＋L1－x甲＝36m
（2）甲车追上乙车时，位移关系x甲′＝x乙′＋L1
甲车位移x甲′＝v甲t2＋，
乙车位移x乙′＝v乙t2，
将x甲′、x乙′代入位移关系，得v甲t2＋＝v乙t2＋L1
代入数值并整理得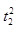
－10t2－11＝0，解得t2＝－1s（舍去）或t2＝11s
此时乙车位移x乙′＝v乙t2＝660m
因x乙′>L2，故乙车已冲过终点线，即到达终点时甲车不能追上乙车