问题
问答题
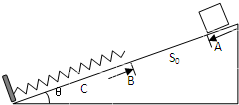
如图,在水平地面上固定一倾角为θ的斜面,一轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.滑块与斜面间动摩擦因素为μ且μ<tanθ,一质量为m的滑块从距离弹簧上端为S0处的A点由静止释放,设滑块与弹簧接触过程中没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g.
(1)求滑块从A点运动到与弹簧上端B点接触瞬间所经历的时间t;
(2)若滑块从B点运动到弹簧形变最大的C点处的距离为L,求滑块第一次能反弹到的最高点离C点的距离X.
答案
(1)滑块运动的加速度a=
=gsinθ-μgcosθmgsinθ-μmgcosθ m
由s0=
at2得1 2
所求时间t=2s0 gsinθ-μgcosθ
故滑块从A点运动到与弹簧上端B点接触瞬间所经历的时间为
.2s0 gsinθ-μgcosθ
(2)滑块从A到C由能量守恒得:mg(s0+L)sinθ=μmgcosθ(s0+L)+Ep…①
滑块从C点第一次反弹到最高点过程有能量守恒得:Ep=mgxsinθ+μmgcosθ•x…②
由①、②两式联立解得x=
.(sinθ-μcosθ)(s0+L) sinθ+μcosθ
故滑块第一次能反弹到的最高点离C点的距离为
.(sinθ-μcosθ)(s0+L) sinθ+μcosθ
