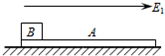
如图所示,A是一个质量为1×10-3kg表面绝缘的薄板,薄板静止在光滑的水平面上,在薄板左端放置一质量为1×10-3kg带电量为q=1×10-5C的绝缘物块,在薄板上方有一水平电场,可以通过开关控制其有、无及方向.先产生一个方向水平向右,大小E1=3×102V/m的电场,薄板和物块开始运动,作用时间2s后,改变电场,电场大小变为E2=1×102V/m,方向向左,电场作用一段时间后,关闭电场,薄板正好到达目的地,物块刚好到达薄板的最右端,且薄板和物块的速度恰好为零.已知薄板与物块间的动摩擦因数µ=0.1,(薄板不带电,物块体积大小不计,g取10m/s2)求:
(1)在电场E1作用下物块和薄板的加速度各为多大;
(2)电场E2作用的时间;
(3)薄板的长度和薄板移动的距离.
(1)根据牛顿第二定律得:物块的加速度a1=
=F1-μmg m
=E1q-μmg m
m/s2=2m/s23×102×1×10-3-0.1×10-3 0.1×10-3
薄板的加速度为:a2=
=1m/s2.μmg M
(2)经t1=2s 物块速度为v1=a1t1=2×2m/s,向右;薄板的加速度v2=a2t1=1×2=2m/s,向右.
经2s后,物块做匀减速运动,加速度大小a1′=
=2m/s2Eq2+μmg m
,向左.薄板的加速度不变,仍为a2=1m/s2向右.当两者速度相等时,货柜恰好到达小车最右端,以后因为qE2=f=µ(m0+m1)g,两者一起作为整体向右以a3=
=0.5m/s2,向右作匀减速直到速度都为0.qE2 M+m
共同速度为v=v1-a1′t2,v=v2+a2′t2
解得 t2=
s,v=2 3
s8 3
物块和薄板获得共同速度直到停止运动用时t3=
=0-v -a3
s16 3
第二次电场作用时间为t=t2+t3=6s
(3)经t1=2s时,物块运动位移为x1=
a1t12=4m 1 2
薄板运动位移x2=
a2t12=2m1 2
薄板在t2时间内位移x3=v2t2+
a2t22=1 2
m14 9
物块在t2时间内位移为x4=v1t2-
a1′t22=1 2
m20 9
薄板的长度L=x1-x2+x4-x3=
m=2.67m24 9
薄板移动的距离为x=x2+x3+
=0-v2 2a3
m=10.67m32 3
答:
(1)在电场E1作用下物块和薄板的加速度各为2m/s2和1m/s2.
(2)电场E2作用的时间是6s;
(3)薄板的长度是2.67m,薄板移动的距离是10.67m.
