问题
解答题
已知y+b与x+a(n、6为常数)成正比例函数,试说明y是x的一次函数.
如果x=3时,y=5;x=2时,y=2,把y表示成x的函数.
答案
解:由题知y+b与x+a(a,b为常数)成正比,
设y+b=k(x+a)(k≠0),则y=kx+ak -b,
∵k≠0,
故y是x的一次函数,
∵如果x=3时,y=5;x =2时,y=2,则
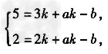
解得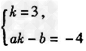
∴y=3x -4.
已知y+b与x+a(n、6为常数)成正比例函数,试说明y是x的一次函数.
如果x=3时,y=5;x=2时,y=2,把y表示成x的函数.
解:由题知y+b与x+a(a,b为常数)成正比,
设y+b=k(x+a)(k≠0),则y=kx+ak -b,
∵k≠0,
故y是x的一次函数,
∵如果x=3时,y=5;x =2时,y=2,则
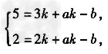
解得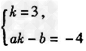
∴y=3x -4.