函数f(x)=cos2x+asinx+a+1,x∈R。
(Ⅰ)设函数f(x)的最小值为g(a),求g(a)的表达式;
(Ⅱ)若对于任意的x∈R,f(x)≥0恒成立,求a的取值范围;
(Ⅲ)若对于任意的a∈[-2,0],f(x)≥0恒成立,求x的取值范围。
解:(Ⅰ)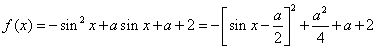 ,
,
①当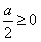 即
即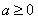 时,函数在sinx=-1处取得最小值,g(a)=1;
时,函数在sinx=-1处取得最小值,g(a)=1;
②当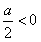 即
即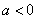 时,函数在sinx=1处取得最小值,g(a)=2a+1,
时,函数在sinx=1处取得最小值,g(a)=2a+1,
综上,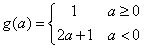 。
。
(Ⅱ)对于任意x∈R,f(x)≥0恒成立,
只需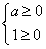 或
或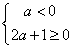 ,
,
解得: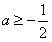 。
。
(Ⅲ)设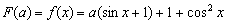 ,
,
所以,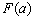 是一次函数,且斜率大于等于零,
是一次函数,且斜率大于等于零,
要使任意的a∈[-2,0],f(x)≥0恒成立,
只需: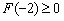 ,即
,即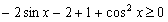 ,
,
整理,得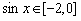 ,即
,即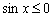 ,
,
所以,x的取值范围是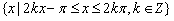 。
。
