问题
解答题
设函数f(x)=ax2+bx+1,a>0,b∈R的最小值为-a,f(x)=0两个实根为x1、x2。
(1)求x1-x2的值;
(2)若关于x的不等式f(x)<0解集为A,函数f(x)+2x在A上不存在最小值,求a的取值范围;
(3)若-2<x1<0,求b的取值范围。
答案
解:(1)∵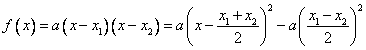 ,
,
∴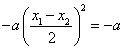 ,∴
,∴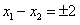 。
。
(2)不妨设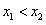 ,
,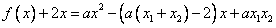 在
在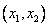 不存在最小值,
不存在最小值,
∴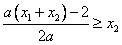 或
或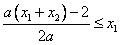 ,
,
又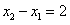 ,a>0,
,a>0,
∴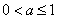
(3)∵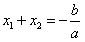 ,
,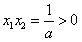 ,
,
∴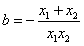 ,
,
又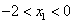 ,∴
,∴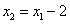 ,
,
∴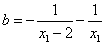 在
在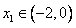 上为增函数,
上为增函数,
∴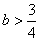 。
。

