问题
单项选择题
若实数x、y满足（x+5）2+（y-12）2=142，则x2+y2的最小值为（）．
A．2
B．1
C．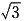
D．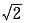
答案
参考答案：B
解析：
实数对(x，y)在以(-5，12)为圆心、14为半径的圆上，x2+y2表示圆上的点到原点的距离的平方，而圆心(-5，12)到坐标原点的距离为13，所以圆上点到原点距离的平方最小值为14-13=1. 故选B．
搜题请搜索小程序“爱下问搜题”
若实数x、y满足（x+5）2+（y-12）2=142，则x2+y2的最小值为（）．
A．2
B．1
C．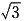
D．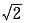
参考答案：B
解析：
实数对(x，y)在以(-5，12)为圆心、14为半径的圆上，x2+y2表示圆上的点到原点的距离的平方，而圆心(-5，12)到坐标原点的距离为13，所以圆上点到原点距离的平方最小值为14-13=1. 故选B．