问题
解答题
已知函数f（x）=x2+ax+3，当x∈[-2，2]时，f（x）≥a恒成立，求a的最小值。
答案
解：设f（x）在[-2，2]上的最小值为g（a），则满足g（a）≥a的a的最小值即为所求，
配方得
，
（1）当
时，
，
由
，解得-6≤a≤2，∴-4≤a≤2；
（2）当
时，g（a）=g（2）=7+2a，由7+2a≥a，得a≥-7，∴
；
（3）当
时，g（a）=g（-2）=7-2a，由7-2a≥a，得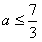
，这与a≥4矛盾，此种情形不存在；
综上讨论，得-7≤a≤2，
∴amin=-7。