问题
解答题
设f(x)=ax2+(b-8)x-a-ab，不等式f(x)＞0的解集是（-3，2）。
（1）求f(x)；
（2）当函数f(x)的定义域是[0，1]时，求函数f(x)的值域。
答案
解：（1）由已知方程f（x）=0的两根为-3和2（a＜0），
由韦达定理得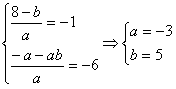
，
从而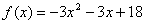
。
（2）
，
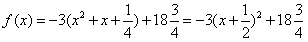而x∈[0，1]，对称轴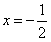
，从而f(x)在[0，1]上为减函数，
所以，当x=0时，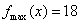
；当x=1时，
；
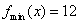故所求函数f(x)的值域为[12，18]。