问题
解答题
已知函数f(x)=x2+2ax+2,x∈[-5,5]。
(1)当a=-1时,求函数的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数,并指出相应的单调性。
答案
解:(1)当a=1时,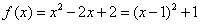 ,
,
函数图象对称轴x=1,
∵x∈[-5,5],
∴ ,
,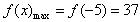 。
。
(2)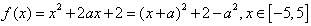 ,
,
对称轴x=-a,
当-a≤-5,即a≥5时,f(x)在[-5,5]上单调递增;
当-a≥5,即a≤-5时,f(x)在[-5,5]上单调递减。
